Co je dělitelné 7?

Jak zjistit jestli je číslo dělitelné

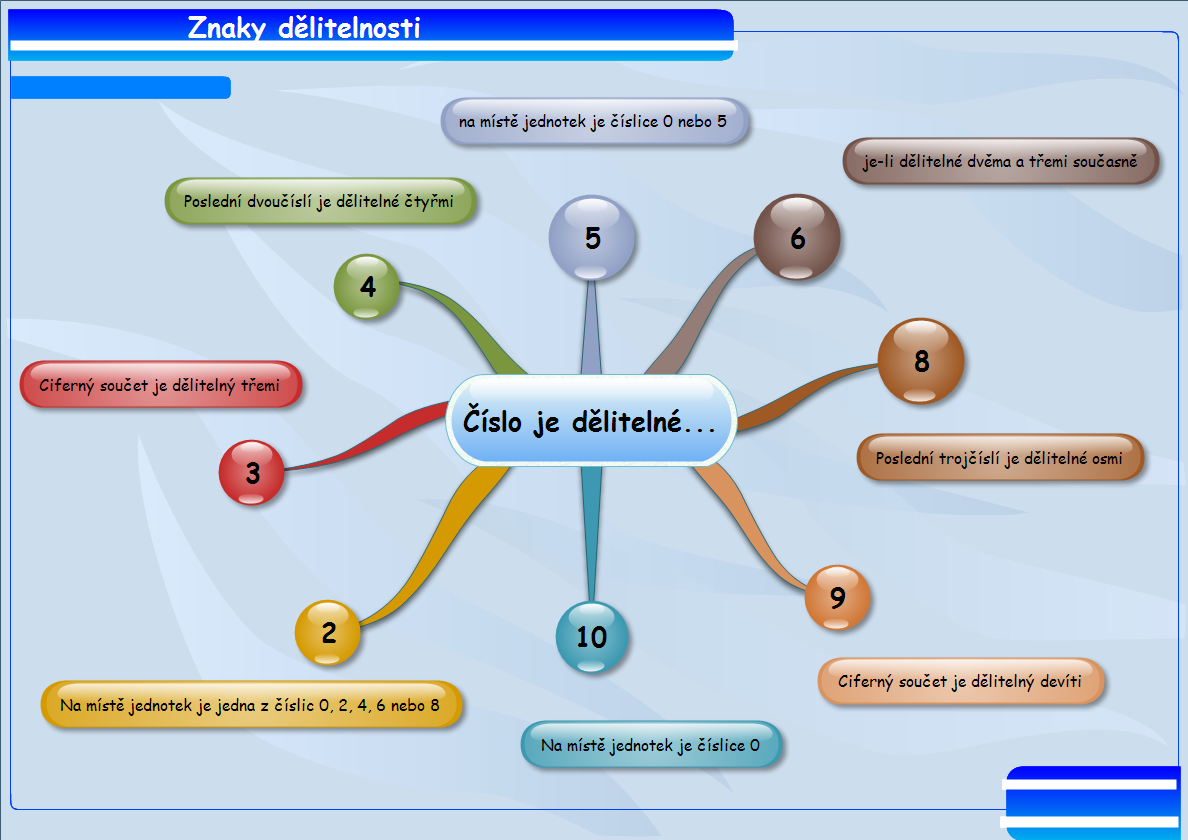
Pravidla dělitelnostiČíslo je dělitelné dvěmi, jestliže je sudé.Číslo je dělitelné třemi, jestliže ciferný součet je dělitelný třemi.Číslo je dělitelné čtyřmi, jestliže je poslední dvojčíslí dělitelné čtyřmi.Číslo je dělitelné pěti, jestliže končí nulou nebo pětkou.

Kdy je číslo dělitelné devíti

9. Číslo je dělitelné devíti, je-li jeho ciferný součet dělitelný devíti.
Archiv

Jak poznat jestli je číslo dělitelné 11

Přirozené číslo je dělitelné 11, právě když rozdíl součtu cifer na lichých pozicích a součtu cifer na sudých pozicích je dělitelný 11.
Archiv

Čím je dělitelné číslo 13

Kritéria dělitelnosti

q	kritérium
12	je-li číslo dělitelné 3 a 4 (viz výše)
13	je-li rozdíl součtů lichých a sudých trojic cifer dělitelný třinácti
14	je-li číslo dělitelné 2 a 7 (viz výše)
15	je-li číslo dělitelné 3 a 5 (viz výše)

Kdy je číslo dělitelné 6

Číslo je dělitelné 6, když je dělitelné dvěma a třemi zároveň. To znamená, že je to sudé číslo a zároveň jeho ciferný součet je dělitelný třemi.

Kdy je číslo dělitelné 5

Přirozené číslo je dělitelné 5, právě když jeho poslední číslice je 0, 5. Přirozené číslo je dělitelné 10, právě když jeho poslední číslice je 0.

Jak poznat že je číslo dělitelné 4

Číslo je dělitelné čtyřmi, jestliže je poslední dvojčíslí dělitelné čtyřmi. (0, 4, 8, 16, 24, … 96, 100, 104, … )

Jak poznám že je číslo dělitelné 6

Číslo je dělitelné 6, když je dělitelné dvěma a třemi zároveň. To znamená, že je to sudé číslo a zároveň jeho ciferný součet je dělitelný třemi.

Jak poznám že je číslo dělitelné 9

Pravidla dělitelnosti čísel

Dělitelnost číslem	Jak poznat
8	Poslední trojčíslí je dělitelné osmi např. 21 320 >> 320 >> ANO
9	Součet cifer je dělitelný devíti např. 3 978 >> 3+9+7+8=27 >> ANO
10	Končí číslicí 0

Čím je dělitelná 17

Pravidla dělitelnosti čísel

Dělitelnost číslem	Jak poznat
17	Poslední cifru vynásobíme pěti a odečteme ji od zbytku čísla (zbylé cifry bez té poslední). Takový výsledek musí být dělitelný sedmnácti. Lze postupně opakovat, až se dostaneme k malým hodnotám. např. 867 >> 86 -7*5 = 86-35 = 51 >> ANO

Čím je dělitelné číslo 47

47 (číslo)

← 46 47 48 →
← 40 41 42 43 44 45 46 47 48 49 →
Celé číslo	47 čtyřicet sedm
Rozklad	prvočíslo
Dělitelé	1, 47

Co je to dělitel

Dělitele jsou celá čísla, která beze zbytku dělí jiné číslo. Díky dělitelům můžeme čísla rozdělit na menší části. Pro představení dělitelů čísla 12 můžeme rozdělit 12 teček do stejně velkých skupin.

Co je triviální dělitel

Každé číslo x je dělitelné čísly 1, −1, x a −x. Tato čísla považujeme za triviální dělitele čísla x. Definici triviálního dělitele ale raději vyslovme trochu jinak: triviální dělitel čísla x je každý dělitel čísla 1, a také každý takový dělitel čísla x, který je současně dělitelný číslem x.

Čím je dělitelná 51

51 (číslo)

← 50 51 52 →
Celé číslo	51 padesát jedna
Rozklad	3 · 17
Dělitelé	1, 3, 17, 51
Římskými číslicemi	LI

Čím se dá dělit 51

51 (číslo)

← 50 51 52 →
Celé číslo	51 padesát jedna
Rozklad	3 · 17
Dělitelé	1, 3, 17, 51
Římskými číslicemi	LI

Čím je dělitelné číslo 61

61 (číslo)

← 60 61 62 →
Celé číslo	61 šedesát jedna
Rozklad	prvočíslo
Dělitelé	1, 61
Římskými číslicemi	LXI

Čím je dělitelné číslo 72

72 (číslo)

← 71 72 73 →
← 70 71 72 73 74 75 76 77 78 79 →
Celé číslo	72 sedmdesát dva
Rozklad	23 · 32
Dělitelé	1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72

Čím se dá dělit 91

91 (číslo)

← 90 91 92 →
Celé číslo	91 devadesát jedna
Rozklad	7 · 13
Dělitelé	1, 7, 13, 91
Římskými číslicemi	XCI

Čím je dělitelné číslo 53

53 (číslo)

← 52 53 54 →
← 50 51 52 53 54 55 56 57 58 59 →
Celé číslo	53 padesát tři
Rozklad	prvočíslo
Dělitelé	1, 53

Čím je dělitelné číslo 87

87 (číslo)

← 86 87 88 →
← 80 81 82 83 84 85 86 87 88 89 →
Celé číslo	87 osmdesát sedm
Rozklad	3 · 29
Dělitelé	1, 3, 29, 87

Čím je dělitelné číslo 27

27 (číslo)

← 26 27 28 →
Rozklad	33
Dělitelé	1, 3, 9, 27
Římskými číslicemi	XXVII
Dvojkově	110112

Čím je dělitelné číslo 51

D 51 = {1, 3, ,51} D 85 = {1, 5, 17, 85} D 102 = {1, 2, 3, 6, 17,34, 51, 102} Vidím, že společným dělitelem všech čísel je jen číslo 1.

Čím je dělitelné číslo 38

38 (číslo)

← 37 38 39 →
← 30 31 32 33 34 35 36 37 38 39 →
Celé číslo	38 třicet osm
Rozklad	2 · 19
Dělitelé	1, 2, 19, 38

Čím je dělitelné číslo 121

121 (číslo)

← 120 121 122 →
← 120 121 122 123 124 125 126 127 128 129 →
Celé číslo	121 sto dvacet jedna
Rozklad	112
Dělitelé	1, 11, 121

Čím je dělitelné číslo 133

133 (číslo)

← 132 133 134 →
← 130 131 132 133 134 135 136 137 138 139 →
Celé číslo	133 sto třicet tři
Rozklad	7 · 19
Dělitelé	1, 7, 19, 133