Jak poznat co je grafem funkce?

Co je graf funkce

Graf nejčastěji zobrazuje závislost y=f(x), popř. z=f(x,y). V případě většího počtu nezávislých proměnných se obvykle používá graf zachycující závislost pouze na vybraných (jedné nebo dvou) proměnných.

Jak poznat že je funkce omezená

Ekvivalentně, funkce f je omezená jestliže existuje číslo h takové, že pro všechna x z definičního oboru D( f ) platí -h ≤ f (x) ≤ h, jinými slovy | f (x)| ≤ h. Omezenost shora znamená, že existuje vodorovná čára tak, že celý graf funkce leží pod ní.
Archiv

Jak vypočítat graf funkce

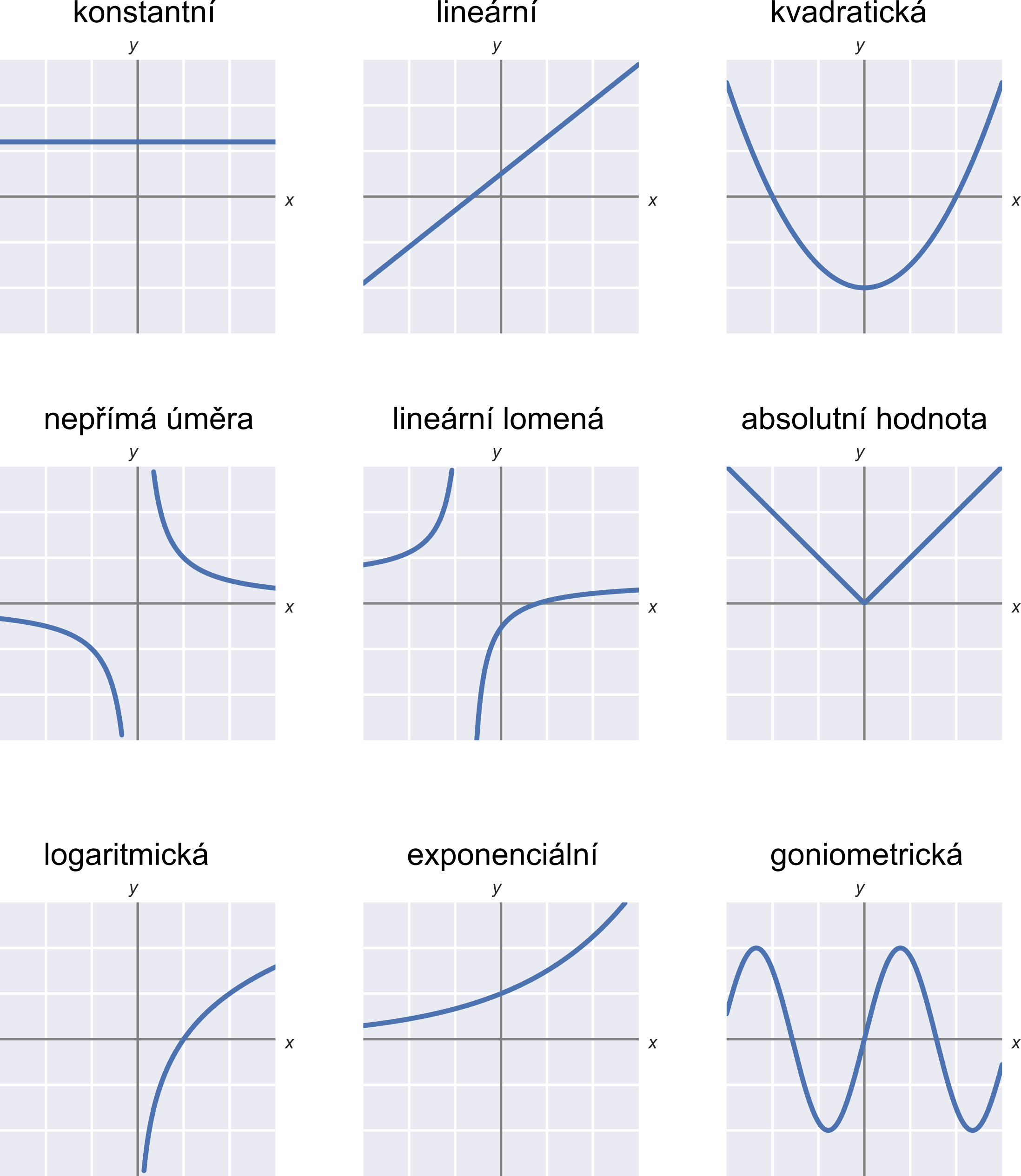
Lineární funkce je dána předpisem y = ax + b (a a b jsou reálná čísla). Grafem je přímka, která prochází body o souřadnicích [0; b], [1; a + b]. Pokud je a > 0 – funkce je rostoucí. Pokud je a < 0 – funkce je klesající.

Co je grafem lineární funkce

Grafem lineární funkce je přímka.

Jak vytvořit graf funkce

Vyberte data, ze kterých chcete vytvořit graf. Klikněte na Vložení > Doporučené grafy. Po výběru typu grafu na kartě Doporučené grafy se vám zobrazí náhled grafu. Poznámka: Můžete vybrat požadovaná data v grafu a stisknutím kláves ALT + F1 vytvořit graf okamžitě, ale nemusí to být nejlepší graf pro data.

Jak nakreslit graf funkce

Graf funkce můžeme samozřejmě vždy nakreslit tak, že spočítáme několik bodů, ale my se budeme soustředit na jisté zajímavé body a na to, jaký má graf přibližně tvar. Zejména nás budou zajímat ty vlastnosti funkce, které lze odhalit pomocí nástrojů diferenciálního počtu, tedy pomocí derivování.

Kdy to není funkce

U funkce to bude vždycky 1 výstup, 1 prvek z oboru hodnot, který se váže na ten prvek z definičního oboru. Pokud bychom měli jeden prvek z definičního oboru, ten bychom vložili do krabičky, která má být funkcí, a dostali bychom ne 1 prvek z oboru hodnot, ale nějaké y, nějaké z, nějaké e, tak toto není funkce.

Jak poznat jestli je funkce sudá nebo lichá

Funkce sudá a lichá

Sudou, anebo lichou funkci poznáme snadno z grafu funkce. Jestliže je graf osově souměrný podle osy y, pak se jedná o funkci sudou. V případě, že je graf funkce středově souměrný podle počátku soustavy souřadnic, pak se jedná o funkci lichou. f(x)=f(-x).

Jak poznat graf lineární funkce

Toto slovo pochází z latinského linea, což označuje čáru nebo přímku. Grafem lineární funkce tedy bude přímka. Předpis lineární funkce je f:y=ax+b. Pomocí koeficientů a a b můžeme ovlivnit vzhled grafu lineární funkce, jestli bude funkce rostoucí, nebo klesající a kde graf protne osu y.

Jak zjistit předpis funkce z grafu

Předpis lineární funkce je f:y=ax+b. Pomocí koeficientů a a b můžeme ovlivnit vzhled grafu lineární funkce, jestli bude funkce rostoucí, nebo klesající a kde graf protne osu y. f:y=ax+b, kde a a b jsou reálná čísla.

Co je grafem kvadratické funkce

Grafem kvadratické funkce je parabola.

Co to je graf

Graf je struktura, která nám pomáhá znázorňovat objekty a vztahy mezi nimi. Skládá se z vrcholů a hran. Vrcholy často reprezentují reálné objekty a obvykle je kreslíme jako tečky nebo kolečka. Hrany představují vztahy mezi vrcholy, na obrázku obvykle vypadají jako čáry mezi vrcholy.

Jak vybrat data do grafu

Klikněte pravým tlačítkem myši na graf a zvolte Vybrat data. Na listu, který obsahuje zdrojová data grafu, se zobrazí dialogové okno Vybrat zdroj dat. Po opuštění dialogového okna klikněte na list a potom kliknutím a přetažením vyberte všechna data, která chcete použít pro graf, včetně nové datové řady.

Kdy je funkce rostoucí

Funkci nazveme rostoucí tehdy, když s rostoucí hodnotou x roste hodnota y. Funkce f je rostoucí, právě když pro všechna x_1,x_2\in D(f) platí: Je-li x_1 < x_2, pak f(x_1) < f(x_2). Na následujícím obrázku je uveden příklad rostoucí funkce. Funkce je klesající tehdy, když s rostoucí hodnotou x klesá hodnota y.

Co plati pro lichou funkcí

Nechť funkce f splňuje následující podmínku: x∈D(x)⇒(−x)∈D(f). Řekneme, že funkce f je sudá pokud platí f(−x)=f(x). Řekneme, že funkce f je lichá pokud platí f(−x)=−f(x).

Co je graf konstantní funkce

Konstantní funkce je periodická, ale nelze určit základní periodu. Konstantní funkce je omezená shora i zdola. Grafem konstantní funkce je přímka rovnoběžná s osou x.

Jak určit předpis funkce

Předpis lineární funkce je f:y=ax+b. Pomocí koeficientů a a b můžeme ovlivnit vzhled grafu lineární funkce, jestli bude funkce rostoucí, nebo klesající a kde graf protne osu y. f:y=ax+b, kde a a b jsou reálná čísla.

Jak zjistit předpis kvadratické funkce

Obecný předpis kvadratické funkce vypadá takto: f(x)=ax2+bx+c, kde a, b, c jsou reálná čísla a platí, že a≠0.

Jak se dělá graf

Vytvoření grafuVyberte data, ze kterých chcete vytvořit graf.Klikněte na Vložení > Doporučené grafy.Po výběru typu grafu na kartě Doporučené grafy se vám zobrazí náhled grafu.Vyberte graf.Vyberte OK.

Jak se dělá graf souvětí

Postup při rozboru složitého souvětíUrčíme počet vět podle počtu přísudků.Označíme věty hlavní a vedlejší.Provedeme grafický nákres: v prvním řádku budou hlavní věty v pořadí v jakém jsou uvedeny, v dalších řádcích zakreslujeme vedlejší věty tak, aby věty závislé byly o řádek níž než věty řídící.

Jak pracovat s grafem

Přidání grafu do dokumentu ve WorduKlikněte na Vložení > Graf.Klikněte na typ grafu a pak poklikejte na požadovaný graf.V zobrazené tabulce nahraďte výchozí data vlastními informacemi.Po dokončení tabulku zavřete.Pokud chcete, můžete pomocí tlačítka Možnosti rozložení

Kde delat grafy

Graf můžete vytvořit v Excelu, Wordu i PowerPointu. Data grafu se ale zadávají a ukládají do listu Excelu.

Jak vypada Suda funkce

Funkce je sudá, pokud splňuje jednoduché pravidlo — když do funkce vložíte prvek x a poté inverzní prvek −x, pak musí funkce vrátit stejnou výslednou hodnotu. Typickou sudou funkcí je funkce f(x) = x2.

Jaké jsou druhy souvětí

Dělíme je na souvětí PODŘADNÉ a souvětí SOUŘADNÉ. SOUVĚTÍ PODŘADNÉ – spojení věty hlavní s jednou nebo více větami vedlejšími. SOUVĚTÍ SOUŘADNÉ – spojení minimálně dvou vět hlavních a libovolného počtu vět vedlejších. Věty hlavní spolu obsahově souvisejí a je mezi nimi významový poměr.

Jak poznat věty v souvětí

Souvětí je spojení dvou a více vět do vyššího větného celku.

Nelze se na ni zeptat jinou větou. Jestliže na větě hlavní závisí věta vedlejší, je věta hlavní větou řídící. Je mluvnicky závislá na jiné větě.